Testing¶
come scrivere del codice corretto e tornare a godersi la vita
Un codice corretto è un codice senza bug e senza errori
bug¶
Un codice ha un bug quando si comporta diversamente da quanto scritto nella sua documentazione.
Nella documentazione va inclusa la documentazione esterna (manuale), quella interna (docstrings) e quella implicita (nome delle funzione ed argomenti).
Sono in generale considerati bug anche i commenti ed i nomi delle variabili che non corrispondono a cosa sta facendo il codice.
la funzione più buggata della storia
SPECIFICA: scrivi una funzione che integri una parabola fra due numeri
def moltiplicazione(nome, cognome):
"""questa funzione divide due numeri"""
# eseguo la sottrazione
esponente = nome[cognome]
return esponente
Il codice è corretto ed esegue bene, ma usarla in un codice reale sarebbe un suicidio!
errore¶
un codice è errato quando si comporta diversamente da quello che la logica per cui è stato scritto prescrive
Ad esempio una funzione di ordinamento che non ordina, oppure in alcuni casi particolari non ordina bene.
buona documentazione¶
prendete spunto dalla documentazione di numpy. non si può chiedere molto altro.
import numpy
print("\n".join(numpy.linalg.eig.__doc__.splitlines()[:20]))
print("\n".join(numpy.linalg.eig.__doc__.splitlines()[20:39]))
print("\n".join(numpy.linalg.eig.__doc__.splitlines()[39:60]))
print("\n".join(numpy.linalg.eig.__doc__.splitlines()[60:80]))
print("\n".join(numpy.linalg.eig.__doc__.splitlines()[80:100]))
print("\n".join(numpy.linalg.eig.__doc__.splitlines()[100:120])) #fine
purezza delle funzioni¶
scrivete funzioni pure.
Una funzione è chiamata pura se, a parità di input, ritorna lo stesso output.
Questo vi permette di essere sicuri che una volta verificata la correttezza di una funzione, questo risultato non cambi.
Questo è anche uno dei motivi per cui le variabili globali sono considerate cattiva pratica
tipi di test possibili¶
Riprendiamo il codice della seconda lezione sugli automi cellulari.
Vogliamo testare la nostra funzione per verificare che si comporti in modo corretto.
Che test possiamo pensare di fare?
test di avanzamento: le modifiche che ho introdotto nel mio codice fanno quello che penso
test di regressione: le modifiche che ho introdotto nel mio codice non cambiano come funziona il resto del codice
test positivi: il mio codice mi da il riultato che mi aspetto
test negativi: il mio codice fallisce quando non rispetto le richieste
strategie di test possibili¶
- test informale
- unit test (test aneddotici)
- property testing
test informali¶
Quando scriviamo una funzione, di solito testiamo se funziona senza problemi.
Questo tipo di test è ovviamente necessario, ma ne incontriamo subito i limiti.
def inc(x):
return x + 1
assert inc(3)==4
assert inc(5)==4
assert inc(6)==4
test aneddotici (unit testing)¶
mi salvo in uno script i test che ho effettuato con degli assert.
Ogni volta che faccio una modifica al mio codice lancio i test per vedere che tutto funzioni.
Se osservo un bug, inserisco un nuovo test che mi garantisca che quel bug non si ripresenti.
in generale voglio almeno un esempio che mi mostri il caso tipico d'uso, più un esempio per ogni caso limite.
Immaginate di scrivere una funzione che vi metta in ordine una lista. Volete testare:
- una lista fuori ordine, come
[1, 3, 2], che dia il risultato[1, 2, 3] - una lista vuota dia in uscita una lista vuota
- una lista già in ordine, come
[1, 2, 3], dia come risultato la stessa lista[1, 2, 3]
e così via, ripetendo per diverse liste.
un'ottima libreria per lo unit testing è pytest.
Pytest è un comando da shell che ricerca le funzioni chiamate test_qualcosa e le esegue tutte, riportandoci i risultati
%cd ~
%%file test_prova.py
def inc(x):
return x + 1
def test_answer_1():
assert inc(3) == 5
def test_answer_2():
assert inc(7) == 7
!pytest test_prova.py
Potrei eseguire il codice di test anche manualmente, ma questo avrebbe diversi svantaggi:
- dovrei eseguire a mano tutte le singole funzioni di test (invece che farle scoprire ed eseguire da pytest)
- alla prima eccezione l'intera procedura si interromperebbe, obbligandomi ad avere una visione parziale. Pytest mi visualizza tutte gli errori
- il risultato dell'assert sarebbe molto meno chiaro, mentre pytest lo decora in modo comprensibile
Pytest può inoltre controllare anche se ci aspettiamo un'eccezione, cosa molto più scomoda con il codice normale
import pytest
def test_zero_division():
with pytest.raises(ZeroDivisionError):
1 / 0
Pytest automatizza già notevolmente la nostra procedura di test, ma dobbiamo scrivere ancora a mano un gran numero di test diversi e simili fra di loro.
Dobbiamo ancora trovare un modo per migliorare: l'ideale sarebbe che il computer generasse i test al posto nostro!
Questo non è possibile in senso letterale, ma ci possiamo arrivare abbastanza vicini.
Test basati sulle proprietà¶
Vado a generalizzare i test che ho scritto in modo aneddotico
Nello unit test:
- per ciascun test:
- per ciascun caso:
- specifico l'input
- specifico il risultato atteso
- per ciascun caso:
Nel property test:
- specifico il tipo di dato in input
- per ciascun test:
- specifico l'invarianza associata a quel test
la libreria che uso genererà in maniera casuale i dati in input secondo le regole che ho specificato, li lancerà contro la funzione e cercherà di romperla in tutti i modi.
Se riesce a violare una proprietà, semplifica l'esempio fino a trovare l'esempio più piccolo possibile che ancora vìola quella proprietà, e ce lo restituisce.
Il property based testing non rimpiazza lo unit testing.
Lo estende e lo rende più potente, mentre allo stesso tempo riduce la quantità di codice triviale che dovete scrivere.
Ovviamente per usarlo dovrete pensare di più, ma non sareste qui se aveste paura di pensare.
La libreria che useremo per i property test si chiama hypothesis.
Hypotesis si appoggia a librerie come pytest per il testing, ma genera in modo automatico i test tramite le strategie, che definiscono come dei dati casuali debbano essere passati alla libreria di test.
%%file test_prova.py
from hypothesis import given
import hypothesis.strategies as st
def inc(x):
if x==5:
return 0
return x + 1
def dec(x):
return x - 1
@given(value=st.integers())
def test_answer_1(value):
print(value)
assert dec(inc(value)) == value
@given(value=st.integers())
def test_answer_2(value):
assert dec(inc(value)) == inc(dec(value))
!pytest test_prova.py
Per arrivare a scrivere i test di proprietà non dobbiamo necessariamente partire da zero, ma possiamo costruirli sulla base degli unit test, usando la strategia just
%%file test_prova.py
def inc(x):
return x + 1
def test_answer_1a():
assert inc(3) == 4
from hypothesis import given
import hypothesis.strategies as st
@given(x=st.just(3))
def test_answer_1b(x):
assert inc(x) == x+1
@given(x=st.floats())
def test_answer_1c(x):
assert inc(x) == x+1
!pytest test_prova.py
Come dicevamo, la matematica sul computer è difficile.
Se volessimo ignorare questo caso, potremmo usare la direttiva assume, che impone il rispetto di una condizione agli esempi forniti.
from math import isnan
from hypothesis import assume
@given(x=st.floats())
def test_answer_1c(x):
assume(not isnan(x))
assert inc(x) == x+1
(Alcuni) Pattern di proprietà da testare¶
gli esempi di proprietà sono basati su quelli presentati in questo sito
proprietà commutativa¶

esistenza di una inversa¶
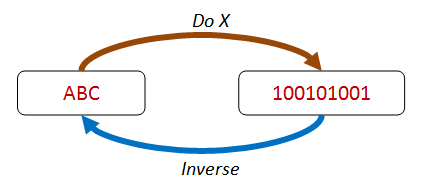
leggi di conservazione¶
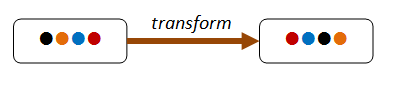
idempotenza¶

induzione¶
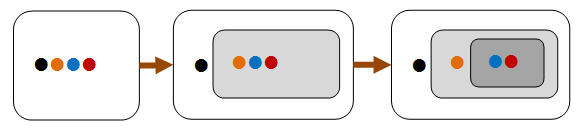
difficile da dimostrare, facile da verificare¶
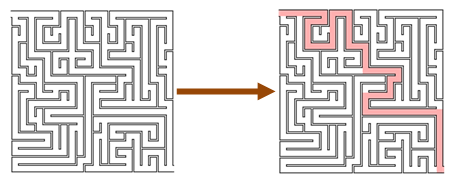
test dell'oracolo¶
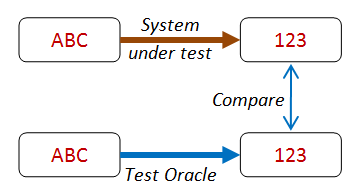
Test Driven Development¶
Nel test driven development, il codice ed i test sono scritti insieme, a partire dalle specifiche. Esistono molte varianti di questo concetto, ma l'idea di base è che non bisogna aspettare di scrivere tutto il codice per iniziare a scrivere i test. Nei casi più estremi si possono addirittura scrivere i test prima ancora del codice!
Nel design di architetture complicate, in cui il design è necessariamente top-down, è una pratica insostituibile.
Automi cellulari, take 2¶
Riprendiamo l'esempio di ieri, cercando di lavorare sulla base di test possibili.
Usiamo quindi l'approcci opposto rispetto a ieri, ovvero un top-down.
Nell'approccio top down svilupperemo il nostro codice fingendo che funzioni tutto bene, poi lo faremo diventare realtà:
- partiamo dalla funzione "finale", richiamando le altre come se esistessero già;
- implementeremo ciascuna funzione come uno "stub", ovvero una versione fasulla, che però ci permette di eseguire il codice;
- scriviamo dei test che rappresentino le proprietà che ci aspettiamo dalle nostre funzioni reali
- rimpiazziamo gli stub con funzioni che approssimino sempre meglio il reale
def simulazione(nsteps):
stato_iniziale = genera_stato()
stati = [stato_iniziale]
for i in range(nsteps):
vecchio_stato = stati[-1]
nuovo_stato = evolvi(vecchio_stato)
stati.append(nuovo_stato)
return stati
notate come non abbia ancora definito in cosa consista la funzione genera_stato e la funzione evolvi.
Ora vado ad implementare degli stubs.
Quali sono le versioni più semplici che possono pensare per far eseguire il mio codice?
Partiamo dall'idea di lavorare su stringhe come ieri (non è obbligatorio, è solo una possibilità)
def genera_stato():
return "stringa"
def evolvi(stato):
return stato
simulazione(5)
Sembra banale, ma ora abbiamo un codice che fa qualcosa, e possiamo migliorarlo incrementalmente invece di cercare di ideare tutto insieme!
Questo approccio ci permette di dividere il problema in sottopassaggi più digeribili, ma richiede di fare qualche assunzione.
Iniziamo ore a scrivere i nostri test.
Partiamo dalla generazione del nostro stato.
Che proprietà vogliamo che abbia?
Ad esempio, potremmo richiedere che i valori possibili siano soltato '.' ed '0'
%%file test_prova.py
def genera_stato():
return "stringa"
def evolvi(stato):
return stato
def simulazione(nsteps):
stato_iniziale = genera_stato()
stati = [stato_iniziale]
for i in range(nsteps):
vecchio_stato = stati[-1]
nuovo_stato = evolvi(vecchio_stato)
stati.append(nuovo_stato)
return stati
########################################################
def test_generazione():
stato = genera_stato()
assert set(stato) == {'.', '0'}
!pytest test_prova.py
%%file test_prova.py
def genera_stato():
return "....00......"
def evolvi(stato):
return stato
def simulazione(nsteps):
stato_iniziale = genera_stato()
stati = [stato_iniziale]
for i in range(nsteps):
vecchio_stato = stati[-1]
nuovo_stato = evolvi(vecchio_stato)
stati.append(nuovo_stato)
return stati
########################################################
def test_generazione():
stato = genera_stato()
assert set(stato) == {'.', '0'}
!pytest test_prova.py
Il nostro test funziona!
Certo, non abbiamo una funzione che genera uno stato interessante, ma intanto genera uno stato valido!
I metodi TDD ci evitano anche di cadere nel trucco della sovraingegnerizzazione.
Non aggiungiamo nuove features al codice finché non ci servono!
La prossima richiesta che potremmo mettere è che non solo contenga solo '.' ed '0', ma che ci sia soltanto uno '0'.
%%file test_prova.py
def genera_stato():
return "....00......"
def evolvi(stato):
return stato
def simulazione(nsteps):
stato_iniziale = genera_stato()
stati = [stato_iniziale]
for i in range(nsteps):
vecchio_stato = stati[-1]
nuovo_stato = evolvi(vecchio_stato)
stati.append(nuovo_stato)
return stati
########################################################
def test_generazione():
stato = genera_stato()
assert set(stato) == {'.', '0'}
def test_generazione():
stato = genera_stato()
num_of_0 = sum(1 for i in stato if i=='0')
assert num_of_0 == 1
!pytest test_prova.py
%%file test_prova.py
def genera_stato():
return ".....0......"
def evolvi(stato):
return stato
def simulazione(nsteps):
stato_iniziale = genera_stato()
stati = [stato_iniziale]
for i in range(nsteps):
vecchio_stato = stati[-1]
nuovo_stato = evolvi(vecchio_stato)
stati.append(nuovo_stato)
return stati
########################################################
def test_generazione():
stato = genera_stato()
assert set(stato) == {'.', '0'}
def test_generazione():
stato = genera_stato()
num_of_0 = sum(1 for i in stato if i=='0')
assert num_of_0 == 1
!pytest test_prova.py